Criteria for Similarity of Triangles
Last Updated :
12 Aug, 2024
Things are often referred similar when the physical structure or patterns they show have similar properties, Sometimes two objects may vary in size but because of their physical similarities, they are called similar objects. For example, a bigger Square will always be similar to a smaller square. In Triangles, if the sizes vary but the shapes they have are alike, then the Triangles can be called Similar Triangles. When two triangles are declared Similar, their corresponding angles are always congruent (Identical in form), and their sides are Proportional. Let's learn more about the similarities of triangles.
Similar Triangles
Two or more than two triangles are similar when their corresponding angles are congruent and their sides are proportional to each other(the ratio of their sides is equal). Noticing things from our daily life or a good look in our textbooks tell us that there are so many objects similar to each other we have never noticed, For Instance, a baby bear looks like its mother even though the mother is relatively bigger, the same concept is applied here in triangles.
 ΔABC and ΔPQR are Similar Triangles
ΔABC and ΔPQR are Similar Triangles Difference between Similar Triangles and Congruent Triangles
- In Similar Triangles, Shape is always same, but Size may vary.
- In Congruent Triangles, Both shape and size are equal.
 ΔABC and ΔPQR are congruent Triangles
ΔABC and ΔPQR are congruent Triangles
Thales Theorem or Basic Proportionality Theorem
A Famous Greek Mathematics “Thales” gave a universal Theorem for Triangles, “In two Triangles that are Equiangular(Corresponding angles of both triangles are equal), the Ratio of their corresponding sides are always equal.”
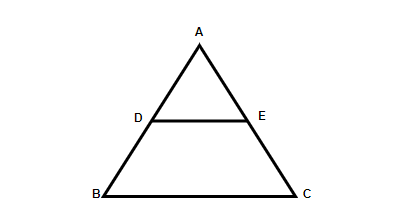 Two Triangles ΔABC and ΔADE shown in one
Two Triangles ΔABC and ΔADE shown in oneAs we can notice, the above given Two triangles are equiangular.
∠A = ∠A [Common Angle]
∠B = ∠D [Corresponding Angles]
∠C = ∠E [Corresponding Angles]
Therefore, it is concluded "If a line is drawn parallel to one side of the triangle to intersect on remaining two sides, it will divide the remaining two sides in the same ratio”
\frac{AD}{AB}=\frac{AE}{AC} , DF//BC
Proof of Thales Theorem
If a line is drawn parallel to one side of a triangle, intersecting other sides at distinct points, then the division of the other two sides is in the same ratio
To Prove:
\frac{AD}{DB}=\frac{AE}{EC}
Given:
In ΔABC, DE is parallel to BC
Construction:
Join BE and CD and draw perpendicular to AC and AB from D and E.
Proof:

In ΔADE, Area of triangle = 1/2 × DE × EN ⇢ 1
Also, 1/2 × DE× DM ⇢ 2
In ΔBDE, Area of Triangle =1/2 × BD × EN ⇢ 3
In ΔDEC, Area of Triangle= 1/2 × EC × DM ⇢ 4
Dividing equation 1 and 3
\frac{area ADE}{area BDE}=\frac{AD}{DB} ⇢ 5
Dividing equation 2 and 4
\\frac{area ADE}{area BDE}= \frac{AE}{EC} ⇢ 6
We know, area of ΔBDE and ΔDEC are equal, since BD is parallel to DE and they both have the same base DE
Now, from equation 5 and 6
\frac{AD}{DB}=\frac{AE}{EC}
Converse of Thales Theorem
If a line divides any two sides of the triangle in the same ratio, then the line is parallel to the third side of the triangle
Proof:

Given:
\frac{PM}{MQ}=\frac{PN}{NR}
Construction:
Lets assume that line MN is not parallel to QR, Draw another line MK such that MK is parallel to QR
Now, in ΔPQR,
\frac{PM}{MQ}=\frac{PK}{KR} ⇢ 1
but, this is also provided that,
\frac{PM}{MQ}=\frac{PN}{NR} ⇢ 2
\frac{PK}{KR}=\frac{PN}{NR}
But, K and N lie on the same line PR, Therefore, they coincide each other and are just the same point.
Therefore, MN and MK are the same line and MN is parallel to QR.
Criteria for Similarity of Triangles
Two triangles are called similar when their angles are equal and their corresponding sides are always in the same ratio, this is what we have learned so far, however one does not need to prove all the things mentioned above to show similarity of two triangles. There are 3 easier ways to find out if the two triangles are similar.
Theorem 1: SSS Similarity Criterion
It states if in a triangle, all the sides are proportional to the sides of other triangles, then the corresponding angles will always be equal and hence, both triangles are Similar.
Proof:

To Prove: \frac{AB}{DE}=\frac{AC}{DF}=\frac{BC}{EF}
Given: ∠A=∠D, ∠B=∠E, ∠C=∠F
Construction: Draw a line PQ in ΔDEF such that AB = DP, AC = DQ, BC = PQ

Proof: \frac{AB}{DE}=\frac{AC}{DF}
\frac{DP}{DE}=\frac{DQ}{DF}
Reciprocal the fraction, \frac{DE}{DP}=\frac{DF}{DQ}
Subtract equation by 1 on both sides\frac{DE}{DP}-1=\frac{DF}{DQ}-1
\frac{PE}{DP}=\frac{QF}{DQ}
By the converse of BPT, PQ is parallel to EF
Therefore, ∠P = ∠E, ∠Q = ∠F (by corresponding angles)
Therefore, ΔDEF∼ ΔDPQ
\frac{DP}{DE}=\frac{DQ}{DF}=\frac{PQ}{EF}
\frac{PQ}{EF}=\frac{BC}{EF}
BC=PQ, AB=DP, AC=DQ
ΔABC≅ ΔDPQ
∠A= ∠D, ∠B= ∠P, ∠C= ∠Q, ∠B= ∠E, ∠C= ∠F,
Hence, ΔABC ∼ ΔDEF
Theorem 2: AAA OR AA Similarity Criterion
AAA referring to angles (all three) of the triangles. It states “If the two corresponding angles both the triangles are equal, then their respective sides will always have same ratio and the triangles are similar triangles”
AA is another name for the theorem since having two angles equal will automatically make the third angle of the triangles equal as the sum is always 180°.
Proof:

Given: ∠A = ∠D, ∠B = ∠E, ∠C = ∠F
To Prove: \frac{AB}{DE}=\frac{AC}{DF}=\frac{BC}{EF}
Construction: Make a line PQ in ΔDEF such that AB=DP, AC=DQ, BC=PQ

Proof: In ΔABC and ΔDPQ
AB=DP, AC=DQ, ∠A=∠D
By S.A.S Property of triangles, both the triangles are congruent to each other.
ΔABC≅ ΔDPQ
We can say, ∠B= ∠DPQ (By CPCT)
∠B= ∠E, Therefore ∠E = ∠DPQ
By corresponding angles, it can be concluded that PQ is parallel to EF
With the help of Converse of Thales theorem,
\frac{DP}{PE}=\frac{DQ}{QF}=\frac{PQ}{EF}
\frac{PE}{DP}=\frac{QF}{DQ}
Adding 1 to both LHS and RHS
\frac{PE+DP}{DP}=\frac{QF+DQ}{DQ}
\frac{DE}{DP}=\frac{QF}{DQ}
Replace DP with AB and DQ with AC
\frac{AB}{DE}=\frac{AC}{DF}
Therefore, the ratio of corresponding sides is coming out to be equal as well.
Hence, ΔABC= ΔDEF
Theorem 3: SAS Similarity Criterion
If the two angles of both the triangles along with both the sides connected to them are equal, then the triangles are called Similar Triangles.
Proof

To Prove: ΔABC∼ ΔDEF
Given: ∠A= ∠D, \frac{AB}{DE}=\frac{AC}{DF}
Construction: Draw a line PQ in triangle ΔDEF Such that AB= DP, AC=DQ

\frac{AB}{DE}=\frac{AC}{DF}
\frac{DP}{DE}=\frac{DQ}{DF}
Reciprocate the fraction, \frac{DE}{DP}=\frac{DF}{DQ}
Subtracting both sides by 1, \frac{PE}{DE}=\frac{QF}{DF}
So, PQ is parallel to EF (by converse of BPT)
∠P= ∠E, ∠Q= ∠F (by corresponding angles)
ΔABC= ΔDPQ
∠A= ∠D, ∠B=∠P, ∠C=∠Q
Since ∠P=∠E, ∠Q= ∠F
Therefore, ∠A=∠D, ∠B= ∠E, ∠C= ∠F
ΔABC∼ ΔDEF
Pythagoras Theorem
In a right-angled Triangle, the square of the hypotenuse is equal to the sum of squares of other two sides
Proof:
Given: ΔPQR is a right angled Triangle and QS is perpendicular to PR
Proof:

We know that, ∠PQR= ∠QSR
∠P= ∠P
Therefore, Δ PQR∼ ΔQSR
\frac{PQ}{QS}=\frac{QR}{RS}=\frac{PR}{QR}
QR2= PR× RS ⇢ 1
Apply the same for Δ PQR and Δ PSQ
PQ2= PR× PS ⇢ 2
From 1 and 2,
PQ2 + QR2= PR× RS + PR× PS
PQ2+ QR2= PR (RS+ PS)
PQ2+ QR2= PR2
Hence, Proved.
Sample Problems
Question 1: In the figure given below, XY is parallel to BC, AX=2cm, XB= 3cm, and the base of the triangle BC= 5cm, Then find the value of XY using Thales Theorem.

Solution:
According to Thales theorem,
\frac{AX}{AB}=\frac{XY}{BC}
\frac{2}{5}=\frac{XY}{5}
{XY}=\frac{10}{5}
XY= 2cm
Question 2: In the right-angled triangle shown below, what is the value of p in terms of q.
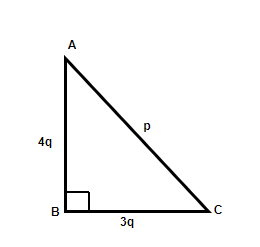
Solution:
ABC is a right-angled triangle,
Using Pythagoras theorem, we get,
AC2= AB2+ BC2
P2= (4q)2+ (3q)2
P2= 16q+ 9q
p2= 25q
p= 5q
Question 3: In the below-given figure, when PQ is parallel to BC, find the value of x.

Solution:
In the Triangle, PQ is parallel to BC, therefore, Thales theorem can be applied,
\frac{AP}{PB}=\frac{AQ}{QC}
\frac{2}{x+2}=\frac{5}{3x-3}
(3x-3)(2)= (x+2)(5)
6x-6= 5x+ 10
x = 16
Question 4: What are the three ways of proving the similarity of Two Triangles?
Answer:
The three ways of Proving Similarity of Triangles are:
- AAA similarity criterion (angle-angle-angle)
- SAS Similarity criterion (side- angle- side)
- SSS similarity criterion (side- side- side)
Question 5: In Triangle ABC, Line DE is drawn in such a way that ∠ABC = ∠DEC, Prove that ΔABC≅ ΔDEC.

Solution:
In ΔABC and ΔDEC,
It is already given that ∠ABC= ∠DEC
And since, angle C is common in both the Triangles, we can say,
∠ACB= ∠DCE
As two angles are equal, the third angle will automatically be equal since the sum of the three angles of a triangle is always 180°
Hence, from AAA Similarity Criterion, it can be concluded,
ΔABC ≅ ΔDEC
Question 6: In a Right-angled isosceles triangle, the base of the triangle is 2cm, Find the hypotenuse of the Triangle.
Solution:
The Triangle given in the question is a right-angled isosceles triangle and shall look something like this.

BC= 2cm
As it is an Isosceles triangle, AB= 2cm,
According to Pythagoras theorem, AC2= AB2 + BC2
AC2= 22+ 22
AC= √8 = 2√2cm
Question 7: How is SAS and SSS Criterion different from each other?
Answer:
Both Criteria have same result, that is, they both proved the triangles to be Congruent to each other, but the method of proving them is very different. In SSS criterion, when all the three sides are known to be equal, then the two Triangles are Congruent in nature. In SAS criterion, when any two sides and the angles between those two sides are equal, then the Triangles are known to be Congruent.
Practice Problems
1. Consider triangles △ABC and △ADE,DE is parallel to BC, AD=4cm, DB=6cm, and the base of the triangle BC=12cm. Find the value of DE using Thales Theorem.
2. In △ABC and △DEF, ∠A=∠D, ∠B=∠E, and ∠C=∠F. Are these two triangles similar? Justify your answer.
3. In △PQR and △STU, PQ=6cm, QR=8cm, RP=10cm, ST=3cm, TU=4cm, and US=5cm. Are these two triangles similar? Justify your answer.
4.In △ABC, D and E are points on AB and AC respectively, such that DE ∥ BC. If AD=3cm, DB=6cm, and AC=12cm, find AE.
Related Articles:
Similar Reads
CBSE Class 10 Maths Notes PDF: Chapter Wise Notes 2024
Math is an important subject in CBSE Class 10th Board exam. So students are advised to prepare accordingly to score well in Mathematics. Mathematics sometimes seems complex but at the same time, It is easy to score well in Math. So, We have curated the complete CBSE Class 10 Math Notes for you to pr
15+ min read
Chapter 1: Real Numbers
Real Numbers
Real Numbers are continuous quantities that can represent a distance along a line, as Real numbers include both rational and irrational numbers. Rational numbers occupy the points at some finite distance and irrational numbers fill the gap between them, making them together to complete the real line
10 min read
Euclid Division Lemma
Euclid's Division Lemma which is one of the fundamental theorems proposed by the ancient Greek mathematician Euclid which was used to prove various properties of integers. The Euclid's Division Lemma also serves as a base for Euclid's Division Algorithm which is used to find the GCD of any two numbe
5 min read
Fundamental Theorem of Arithmetic
The Fundamental Theorem of Arithmetic is a useful method to understand the prime factorization of any number. The factorization of any composite number can be uniquely written as a multiplication of prime numbers, regardless of the order in which the prime factors appear. The figures above represent
7 min read
HCF / GCD and LCM - Definition, Formula, Full Form, Examples
The full form of HCF is the Highest Common Factor while the full form of LCM is the Least Common Multiple. HCF is the largest number that divides two or more numbers without leaving a remainder, whereas LCM is the smallest multiple that is divisible by two or more integers. Table of Content HCF or G
10 min read
Irrational Numbers- Definition, Examples, Symbol, Properties
Irrational numbers are real numbers that cannot be expressed as fractions. Irrational Numbers can not be expressed in the form of p/q, where p and q are integers and q ≠0. They are non-recurring, non-terminating, and non-repeating decimals. Irrational numbers are real numbers but are different from
12 min read
Decimal Expansions of Rational Numbers
Real numbers are simply the combination of rational and irrational numbers, in the number system. In general, all the arithmetic operations can be performed on these numbers and they can be represented in the number line, also. So in this article let's discuss some rational and irrational numbers an
6 min read
Rational Numbers
Rational numbers are a fundamental concept in mathematics, defined as numbers that can be expressed as the ratio of two integers, where the denominator is not zero. Represented in the form p/q​ (with p and q being integers), rational numbers include fractions, whole numbers, and terminating or repea
15+ min read
Chapter 2: Polynomials
Algebraic Expressions in Math: Definition, Example and Equation
Algebraic Expression is a mathematical expression that is made of numbers, and variables connected with any arithmetical operation between them. Algebraic forms are used to define unknown conditions in real life or situations that include unknown variables. An algebraic expression is made up of term
8 min read
Polynomial Formula
The polynomial Formula gives the standard form of polynomial expressions. It specifies the arrangement of algebraic expressions according to their increasing or decreasing power of variables. The General Formula of a Polynomial: f(x) = an​xn + an−1​xn−1 + ⋯ + a1​x + a0​ Where, an​, an−1​, …, a1​, a0
6 min read
Types of Polynomials (Based on Terms and Degrees)
Types of Polynomials: In mathematics, an algebraic expression is an expression built up from integer constants, variables, and algebraic operations. There are mainly four types of polynomials based on degree-constant polynomial (zero degree), linear polynomial ( 1st degree), quadratic polynomial (2n
9 min read
Zeros of Polynomial
Zeros of a Polynomial are those real, imaginary, or complex values when put in the polynomial instead of a variable, the result becomes zero (as the name suggests zero as well). Polynomials are used to model some physical phenomena happening in real life, they are very useful in describing situation
14 min read
Geometrical meaning of the Zeroes of a Polynomial
An algebraic identity is an equality that holds for any value of its variables. They are generally used in the factorization of polynomials or simplification of algebraic calculations. A polynomial is just a bunch of algebraic terms added together, for example, p(x) = 4x + 1 is a degree-1 polynomial
8 min read
Factorization of Polynomial
Factorization in mathematics refers to the process of expressing a number or an algebraic expression as a product of simpler factors. For example, the factors of 12 are 1, 2, 3, 4, 6, and 12, and we can express 12 as 12 = 1 × 12, 2 × 6, or 4 × 3. Similarly, factorization of polynomials involves expr
10 min read
Division Algorithm for Polynomials
Polynomials are those algebraic expressions that contain variables, coefficients, and constants. For Instance, in the polynomial 8x2 + 3z - 7, in this polynomial, 8,3 are the coefficients, x and z are the variables, and 7 is the constant. Just as simple Mathematical operations are applied on numbers
5 min read
Algebraic Identities
Algebraic Identities are fundamental equations in algebra where the left-hand side of the equation is always equal to the right-hand side, regardless of the values of the variables involved. These identities play a crucial role in simplifying algebraic computations and are essential for solving vari
14 min read
Relationship between Zeroes and Coefficients of a Polynomial
Polynomials are algebraic expressions with constants and variables that can be linear i.e. the highest power o the variable is one, quadratic and others. The zeros of the polynomials are the values of the variable (say x) that on substituting in the polynomial give the answer as zero. While the coef
9 min read
Division Algorithm Problems and Solutions
Polynomials are made up of algebraic expressions with different degrees. Degree-one polynomials are called linear polynomials, degree-two are called quadratic and degree-three are called cubic polynomials. Zeros of these polynomials are the points where these polynomials become zero. Sometimes it ha
6 min read
Chapter 3: Pair of Linear equations in two variables
Linear Equation in Two Variables
Linear Equation in Two Variables: A Linear equation is defined as an equation with the maximum degree of one only, for example, ax = b can be referred to as a linear equation, and when a Linear equation in two variables comes into the picture, it means that the entire equation has 2 variables presen
9 min read
Pair of Linear Equations in Two Variables
Linear Equation in two variables are equations with only two variables and the exponent of the variable is 1. This system of equations can have a unique solution, no solution, or an infinite solution according to the given initial condition. Linear equations are used to describe a relationship betwe
11 min read
Graphical Methods of Solving Pair of Linear Equations in Two Variables
A system of linear equations is just a pair of two lines that may or may not intersect. The graph of a linear equation is a line. There are various methods that can be used to solve two linear equations, for example, Substitution Method, Elimination Method, etc. An easy-to-understand and beginner-fr
8 min read
Solve the Linear Equation using Substitution Method
A linear equation is an equation where the highest power of the variable is always 1. Its graph is always a straight line. A linear equation in one variable has only one unknown with a degree of 1, such as: 3x + 4 = 02y = 8m + n = 54a – 3b + c = 7x/2 = 8There are mainly two methods for solving simul
11 min read
Solving Linear Equations Using the Elimination Method
If an equation is written in the form ax + by + c = 0, where a, b, and c are real integers and the coefficients of x and y, i.e. a and b, are not equal to zero, it is said to be a linear equation in two variables. For example, 3x + y = 4 is a linear equation in two variables- x and y. The numbers th
10 min read
Chapter 4: Quadratic Equations
Quadratic Equations
A Quadratic equation is a second-degree polynomial equation that can be represented as ax2 + bx + c = 0. In this equation, x is an unknown variable, a, b, and c are constants, and a is not equal to 0. The solutions of a quadratic equation are known as its roots. These roots can be found using method
11 min read
Roots of Quadratic Equation
The roots of a quadratic equation are the values of x that satisfy the equation. The roots of a quadratic equation are also called zeros of a quadratic equation. A quadratic equation is generally in the form: ax2 + bx + c = 0 Where: a, b, and c are constants (with a ≠0).x represents the variable. T
13 min read
Solving Quadratic Equations
A quadratic equation, typically in the form ax² + bx + c = 0, can be solved using different methods including factoring, completing the square, quadratic formula, and the graph method. While Solving Quadratic Equations we try to find a solution that represent the points where this the condition Q(x)
8 min read
How to find the Discriminant of a Quadratic Equation?
Algebra can be defined as the branch of mathematics that deals with the study, alteration, and analysis of various mathematical symbols. It is the study of unknown quantities, which are often depicted with the help of variables in mathematics. Algebra has a plethora of formulas and identities for th
4 min read
Chapter 5: Arithmetic Progressions
Arithmetic Progressions Class 10- NCERT Notes
Arithmetic Progressions (AP) are fundamental sequences in mathematics where each term after the first is obtained by adding a constant difference to the previous term. Understanding APs is crucial for solving problems related to sequences and series in Class 10 Mathematics. These notes cover the ess
7 min read
Sequences and Series
A sequence is an ordered list of numbers following a specific rule. Each number in a sequence is called a "term." The order in which terms are arranged is crucial, as each term has a specific position, often denoted as an​, where n indicates the position in the sequence. For example: 2, 5, 8, 11, 14
7 min read
Arithmetic Progression in Maths
Arithmetic Progression (AP) or Arithmetic Sequence is simply a sequence of numbers such that the difference between any two consecutive terms is constant. Some Real World Examples of AP Natural Numbers: 1, 2, 3, 4, 5, . . . with a common difference 1Even Numbers: 2, 4, 6, 8, 10, . . . with a common
3 min read
Arithmetic Progression - Common difference and Nth term | Class 10 Maths
Arithmetic Progression is a sequence of numbers where the difference between any two successive numbers is constant. For example 1, 3, 5, 7, 9....... is in a series which has a common difference (3 - 1) between two successive terms is equal to 2. If we take natural numbers as an example of series 1,
5 min read
How to find the nth term of an Arithmetic Sequence?
Answer - Use the formula: an = a1 + (n - 1)dWhere:an = nth term,a = first term,d = common difference,n = term number. Substitute the values of a, d, and n into the formula to calculate an. Steps to find the nth Term of an Arithmetic SequenceStep 1: Identify the First and Second Term: 1st and 2nd ter
3 min read
Arithmetic Progression | Sum of First n Terms | Class 10 Maths
Arithmetic Progression is a sequence of numbers where the difference between any two successive numbers is constant. For example 1, 3, 5, 7, 9……. is in a series which has a common difference (3 – 1) between two successive terms is equal to 2. If we take natural numbers as an example of series 1, 2,
8 min read
Arithmetic Mean
Arithmetic Mean, commonly known as the average, is a fundamental measure of central tendency in statistics. It is defined as the ratio of all the values or observations to the total number of values or observations. Arithmetic Mean is one of the fundamental formulas used in mathematics and it is hig
13 min read
Arithmetic Progression | Sum of First n Terms | Class 10 Maths
Arithmetic Progression is a sequence of numbers where the difference between any two successive numbers is constant. For example 1, 3, 5, 7, 9……. is in a series which has a common difference (3 – 1) between two successive terms is equal to 2. If we take natural numbers as an example of series 1, 2,
8 min read
Chapter 6: Triangles
Triangles in Geometry
A triangle is a polygon with three sides (edges), three vertices (corners), and three angles. It is the simplest polygon in geometry, and the sum of its interior angles is always 180°. A triangle is formed by three line segments (edges) that intersect at three vertices, creating a two-dimensional re
13 min read
Similar Triangles
Similar Triangles are triangles with the same shape but can have variable sizes. Similar triangles have corresponding sides in proportion to each other and corresponding angles equal to each other. Similar triangles are different from congruent triangles. Two congruent figures are always similar, bu
15+ min read
Criteria for Similarity of Triangles
Things are often referred similar when the physical structure or patterns they show have similar properties, Sometimes two objects may vary in size but because of their physical similarities, they are called similar objects. For example, a bigger Square will always be similar to a smaller square. In
9 min read
Basic Proportionality Theorem (BPT) Class 10 | Proof and Examples
Basic Proportionality Theorem: Thales theorem is one of the most fundamental theorems in geometry that relates the parts of the length of sides of triangles. The other name of the Thales theorem is the Basic Proportionality Theorem or BPT. BPT states that if a line is parallel to a side of a triangl
8 min read
Pythagoras Theorem | Formula, Proof and Examples
Pythagoras Theorem explains the relationship between the three sides of a right-angled triangle and helps us find the length of a missing side if the other two sides are known. It is also known as the Pythagorean theorem. It states that in a right-angled triangle, the square of the hypotenuse is equ
10 min read
Chapter 7: Coordinate Geometry
Coordinate Geometry
Coordinate geometry is a branch of mathematics that combines algebra and geometry using a coordinate plane. It helps us represent points, lines, and shapes with numbers and equations, making it easier to analyze their positions, distances, and relationships. From plotting points to finding the short
3 min read
Distance Formula Class 10 Maths
The distance formula is one of the important concepts in coordinate geometry which is used widely. By using the distance formula we can find the shortest distance i.e drawing a straight line between points. There are two ways to find the distance between points: Pythagorean theoremDistance formulaTa
9 min read
Distance Between Two Points
Distance Between Two Points is the length of line segment that connects any two points in a coordinate plane in coordinate geometry. It can be calculated using a distance formula for 2D or 3D. It represents the shortest path between two locations in a given space. In this article, we will learn how
6 min read
Section Formula
Section Formula is a useful tool in coordinate geometry, which helps us find the coordinate of any point on a line which is dividing the line into some known ratio. Suppose a point divides a line segment into two parts which may be equal or not, with the help of the section formula we can find the c
14 min read
How to find the ratio in which a point divides a line?
Answer: To find the ratio in which a point divides a line we use the following formula [Tex]x = \frac{m_1x_2+m_2x_1}{m_1+m_2}Â Â [/Tex][Tex]y = \frac{m_1y_2+m_2y_1}{m_1+m_2}[/Tex]Geo means Earth and metry means measurement. Geometry is a branch of mathematics that deals with distance, shapes, sizes, r
4 min read
How to find the Trisection Points of a Line?
To find the trisection points of a line segment, you need to divide the segment into three equal parts. This involves finding the points that divide the segment into three equal lengths. In this article, we will answer "How to find the Trisection Points of a Line?" in detail including section formul
4 min read
How to find the Centroid of a Triangle?
Answer: The Centroid for the triangle is calculated using the formula[Tex]\left (\frac{[x1+x2+x3]}{3}, \frac{[y1+y2+y3]}{3}\right)[/Tex]A triangle consists of three sides and three interior angles. Centroid refers to the center of an object. Coming to the centroid of the triangle, is defined as the
4 min read
Area of a Triangle in Coordinate Geometry
There are various methods to find the area of the triangle according to the parameters given, like the base and height of the triangle, coordinates of vertices, length of sides, etc. In this article, we will discuss the method of finding area of any triangle when its coordinates are given. Area of T
6 min read
Chapter 8: Introduction to Trigonometry
Trigonometric Ratios
There are three sides of a triangle Hypotenuse, Adjacent, and Opposite. The ratios between these sides based on the angle between them is called Trigonometric Ratio. The six trigonometric ratios are: sine (sin), cosine (cos), tangent (tan), cotangent (cot), cosecant (cosec), and secant (sec). As giv
4 min read
Unit Circle: Definition, Formula, Diagram and Solved Examples
Unit Circle is a Circle whose radius is 1. The center of unit circle is at origin(0,0) on the axis. The circumference of Unit Circle is 2π units, whereas area of Unit Circle is π units2. It carries all the properties of Circle. Unit Circle has the equation x2 + y2 = 1. This Unit Circle helps in defi
7 min read
Trigonometric Ratios of Some Specific Angles
Trigonometry is all about triangles or to be more precise the relationship between the angles and sides of a triangle (right-angled triangle). In this article, we will be discussing the ratio of sides of a right-angled triangle concerning its acute angle called trigonometric ratios of the angle and
6 min read
Trigonometric Identities
Trigonometric identities play an important role in simplifying expressions and solving equations involving trigonometric functions. These identities, which involve relationships between angles and sides of triangles, are widely used in fields like geometry, engineering, and physics. In this article,
10 min read
Chapter 9: Some Applications of Trigonometry